【科技前沿】第15期：微分动力系统孤立周期解分支及其应用研究进展​

【编者按】为了更好地营造校园学术氛围，传播我校学术科研动态，即日起，学校在校园网开辟“科技前沿”专栏，定期总结、回顾学校师生取得的科研成果。欢迎广大师生及时把自己的学术科研成果以邮件的形式告诉我们，我们希望获得您以下成果信息：为政府、企业、媒体进行了专业咨询；科技成果通过了相关鉴定；科技成果落地、实现产业化；发表了高水平的学术论文；获得了专利授权；出版、编著了专著、教材；获得了科技奖励；在重要学术会议上进行了发言……

我们愿意为有学术追求的师生搭建一个交流的平台，希望在师生的努力下，学校的学术氛围日益浓厚，让我们为实现电子信息特色鲜明的高水平大学而奋斗。联系邮箱：dwxcb@guet.edu.cn。

近日，我校数学与计算科学学院王勤龙教授研究团队与加拿大西安大略大学郁培教授在国际权威学术期刊《Journal of Differential Equations》正式发表了题为“Isolated periodic wave solutions arising from Hopf and Poincare bifurcations in a class of single species model”的学术论文，《Journal of Differential Equations》是Elsevier出版社旗下数学学科Top期刊， 2021年影响因子为2.430。

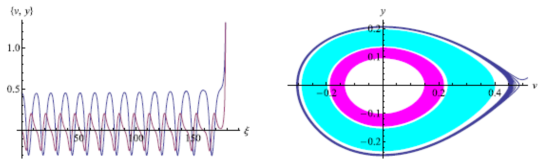
极限环也即孤立周期解的存在与稳定性问题，广泛存在于物理学、力学、生物学、电子学和金融学等自然科学和工程领域，不仅是非线性动力学研究的重要课题，也是微分模型应用研究的重要内容。然而，对于极限环分支问题来说，著名的希尔伯特第十六问题至今依然是一个迷，由阿诺尔德（V.I.Arnold）所提出其弱化问题，即关于阿贝尔积分孤立零点个数对应全局极限环分支数目的问题，已经取得了许多进展，但还存在大量未解决的难题，原因在于现存方法只对某些情况有效，并且需要配合一些特殊的技巧，因此，寻求新的更有效的方法，是研究取得实质进展的关键。

该论文拓展了生物入侵的一类单种群反应扩散模型，基于共轭对称复系统的奇点量算法，讨论了该模型对应二维行波系统所有平衡点的Hopf分支及其中心条件，并由此构造一类扰动哈密顿系统来研究此模型的庞卡莱全局分支。基于切比雪夫准则和严格符号计算，发展利用了二元函数符号不变域的判定方法，有效探索和证明了该模型系统在分段连续参数区间内存在且至多存在两个极限环的结论，并通过数值模拟对结果进行了验证。该结论表明：在具有密度依赖迁移和Allee效应的单种群模型中能够同时存在两个大幅的振荡，它们对应着种群孤立周期行波的两互异时空运动模式，这一新的发现也恰好解释了生物种群动力学性质的复杂性，该文所用方法可以很好地运用到其它问题的解决。

该研究工作得到了国家自然科学基金、广西自然科学基金等资助。